Find eigenvalues of a symmetric matrix. More...

#include <vnl/vnl_matrix.h>
#include <vnl/vnl_diag_matrix.h>

Classes
class	vnl_symmetric_eigensystem< T >
	Computes and stores the eigensystem decomposition of a symmetric matrix. More...
Defines
#define	VNL_SYMMETRIC_EIGENSYSTEM_INSTANTIATE(T) extern "please include vnl/algo/vnl_symmetric_eigensystem.txx first"
Functions
template<class T >
void	vnl_symmetric_eigensystem_compute_eigenvals (T M11, T M12, T M13, T M22, T M23, T M33, T &l1, T &l2, T &l3)
	Find eigenvalues of a symmetric 3x3 matrix.
template<class T >
bool	vnl_symmetric_eigensystem_compute (vnl_matrix< T > const &A, vnl_matrix< T > &V, vnl_vector< T > &D)
	Find eigenvalues of a symmetric matrix.

Detailed Description

Find eigenvalues of a symmetric matrix.

vnl_symmetric_eigensystem_compute() solves the eigenproblem 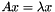$A x = \lambda x$ , with 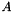$A$ symmetric. The resulting eigenvectors and values are sorted in increasing order so V.column(0) is the eigenvector corresponding to the smallest eigenvalue.

As a matrix decomposition, this is 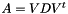$A = V D V^t$

Uses the EISPACK routine RS, which in turn calls TRED2 to reduce A to tridiagonal form, followed by TQL2, to find the eigensystem. This is summarized in Golub and van Loan, pgf 8.2. The following are the original subroutine headers:

Remarks:: TRED2 is a translation of the Algol procedure tred2, Num. Math. 11, 181-195(1968) by Martin, Reinsch, and Wilkinson. Handbook for Auto. Comp., Vol.ii-Linear Algebra, 212-226(1971).; This subroutine reduces a real symmetric matrix to a symmetric tridiagonal matrix using and accumulating orthogonal similarity transformations.; TQL2 is a translation of the Algol procedure tql2, Num. Math. 11, 293-306(1968) by Bowdler, Martin, Reinsch, and Wilkinson. Handbook for Auto. Comp., Vol.ii-Linear Algebra, 227-240(1971).; This subroutine finds the eigenvalues and eigenvectors of a symmetric tridiagonal matrix by the QL method. the eigenvectors of a full symmetric matrix can also be found if tred2 has been used to reduce this full matrix to tridiagonal form.

Author:: Andrew W. Fitzgibbon, Oxford RRG

Date:: 29 Aug 96

    Modifications
     fsm, 5 March 2000: templated
     dac (Manchester) 28/03/2001: tidied up documentation
     Feb.2002 - Peter Vanroose - brief doxygen comment placed on single line
     Jan.2003 - Peter Vanroose - added missing implementation for solve(b,x)
     Mar.2010 - Peter Vanroose - also made vnl_symmetric_eigensystem_compute()
                                 & vnl_symmetric_eigensystem_compute_eigenvals() templated

Definition in file vnl_symmetric_eigensystem.h.

Define Documentation

#define VNL_SYMMETRIC_EIGENSYSTEM_INSTANTIATE ( T ) extern "please include vnl/algo/vnl_symmetric_eigensystem.txx first"

Definition at line 142 of file vnl_symmetric_eigensystem.h.

Function Documentation

template<class T >

bool vnl_symmetric_eigensystem_compute	(	vnl_matrix< T > const &	A,
		vnl_matrix< T > &	V,
		vnl_vector< T > &	D
	)

Find eigenvalues of a symmetric matrix.

Definition at line 95 of file vnl_symmetric_eigensystem.txx.

template<class T >

void vnl_symmetric_eigensystem_compute_eigenvals	(	T	M11,
		T	M12,
		T	M13,
		T	M22,
		T	M23,
		T	M33,
		T &	l1,
		T &	l2,
		T &	l3
	)

Find eigenvalues of a symmetric 3x3 matrix.

Eigenvalues will be returned so that l1 <= l2 <= l3.

   Matrix is   M11  M12  M13
               M12  M22  M23
               M13  M23  M33

   Matrix is   M11  M12  M13
               M12  M22  M23
               M13  M23  M33

Definition at line 30 of file vnl_symmetric_eigensystem.txx.

Classes

Defines

Functions

Detailed Description

Define Documentation

Function Documentation