Complete and incomplete gamma function approximations. More...
#include <vcl_cmath.h>Go to the source code of this file.
Functions | |
| double | vnl_log_gamma (double x) |
| Approximate log of gamma function. | |
| double | vnl_gamma (double x) |
| Approximate gamma function. | |
| double | vnl_gamma_p (double a, double x) |
| Normalised Incomplete gamma function, P(a,x). | |
| double | vnl_gamma_q (double a, double x) |
| Normalised Incomplete gamma function, Q(a,x). | |
| double | vnl_cum_prob_chi2 (int n_dof, double chi2) |
| P(chi<chi2). | |
| double | vnl_digamma (double x) |
| approximate digamma function, dLog[gamma[z]]/dz. | |
Detailed Description
Complete and incomplete gamma function approximations.
Definition in file vnl_gamma.h.
Function Documentation
| double vnl_cum_prob_chi2 | ( | int | n_dof, |
| double | chi2 | ||
| ) | [inline] |
P(chi<chi2).
Calculates the probability that a value generated at random from a chi-square distribution with given degrees of freedom is less than the value chi2
- Parameters:
-
n_dof Number of degrees of freedom chi2 Value of chi-squared
Definition at line 39 of file vnl_gamma.h.
| double vnl_digamma | ( | double | x | ) |
approximate digamma function, dLog[gamma[z]]/dz.
Analytic derivative of the Lanczos approximation. Error < 10^-11 1<z<20.
Definition at line 115 of file vnl_gamma.cxx.
| double vnl_gamma | ( | double | x | ) | [inline] |
Approximate gamma function.
Uses 6 parameter Lanczos approximation as described by Toth (http://www.rskey.org/gamma.htm) Accurate to about one part in 3e-11.
Definition at line 21 of file vnl_gamma.h.
| double vnl_gamma_p | ( | double | a, |
| double | x | ||
| ) |
Normalised Incomplete gamma function, P(a,x).
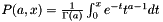 Note the order of parameters - this is the normal maths order. MATLAB uses gammainc(x,a), ie the other way around
Note the order of parameters - this is the normal maths order. MATLAB uses gammainc(x,a), ie the other way around
Definition at line 93 of file vnl_gamma.cxx.
| double vnl_gamma_q | ( | double | a, |
| double | x | ||
| ) |
| double vnl_log_gamma | ( | double | x | ) |
Approximate log of gamma function.
Uses 6 parameter Lanczos approximation as described by Toth (http://www.rskey.org/gamma.htm) Accurate to about one part in 3e-11.
Approximate log of gamma function.
Uses 6 parameter Lanczos approximation as described by Viktor Toth (http://www.rskey.org/gamma.htm) Accurate to about 3e-11.
Definition at line 19 of file vnl_gamma.cxx.
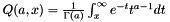
 1.7.5.1
1.7.5.1