core/vnl/vnl_gamma.cxx File Reference

Complete and incomplete gamma function approximations. More...

#include "vnl_gamma.h"
#include <vcl_iostream.h>
#include <vcl_cassert.h>

Go to the source code of this file.

Functions
double	vnl_log_gamma (double x)
	Approximate gamma function.
double	vnl_gamma_p (double a, double x)
	Normalised Incomplete gamma function, P(a,x).
double	vnl_gamma_q (double a, double x)
	Normalised Incomplete gamma function, Q(a,x).
double	vnl_digamma (double z)
	approximate digamma function, dLog[gamma[z]]/dz.
Variables
const int	MAX_ITS = 100
const double	MaxRelError = 3.0e-7
const double	vnl_very_small = 1.0e-30

---

Detailed Description

Complete and incomplete gamma function approximations.

Author:

Tim Cootes

Definition in file vnl_gamma.cxx.

---

Function Documentation

double vnl_digamma

(

double

x

)

approximate digamma function, dLog[gamma[z]]/dz.

Analytic derivative of the Lanczos approximation. Error < 10^-11 1<z<20.

Definition at line 115 of file vnl_gamma.cxx.

double vnl_gamma_p	(	double	a,
		double	x
	)

Normalised Incomplete gamma function, P(a,x).

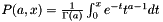Note the order of parameters - this is the normal maths order. MATLAB uses gammainc(x,a), ie the other way around

Definition at line 93 of file vnl_gamma.cxx.

double vnl_gamma_q	(	double	a,
		double	x
	)

Normalised Incomplete gamma function, Q(a,x).

Definition at line 104 of file vnl_gamma.cxx.

double vnl_log_gamma

(

double

x

)

Approximate gamma function.

Approximate log of gamma function.

Uses 6 parameter Lanczos approximation as described by Viktor Toth (http://www.rskey.org/gamma.htm) Accurate to about 3e-11.

Definition at line 19 of file vnl_gamma.cxx.

---

Variable Documentation

const int MAX_ITS = 100

Definition at line 33 of file vnl_gamma.cxx.

const double MaxRelError = 3.0e-7

Definition at line 34 of file vnl_gamma.cxx.

const double vnl_very_small = 1.0e-30

Definition at line 35 of file vnl_gamma.cxx.