Holds the singular value decomposition of a vnl_matrix_fixed. More...
#include <vnl_svd_fixed.h>
Public Types | |
| typedef vnl_numeric_traits< T > ::abs_t | singval_t |
| The singular values of a matrix of complex<T> are of type T, not complex<T>. | |
Public Member Functions | |
| vnl_svd_fixed (vnl_matrix_fixed< T, R, C > const &M, double zero_out_tol=0.0) | |
Construct a vnl_svd_fixed<T> object from 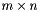 matrix matrix 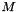 . . | |
| ~vnl_svd_fixed () | |
| void | zero_out_absolute (double tol=1e-8) |
| find weights below threshold tol, zero them out, and update W_ and Winverse_. | |
| void | zero_out_relative (double tol=1e-8) |
| find weights below tol*max(w) and zero them out. | |
| int | singularities () const |
| unsigned int | rank () const |
| singval_t | well_condition () const |
| singval_t | determinant_magnitude () const |
| Calculate determinant as product of diagonals in W. | |
| singval_t | norm () const |
| vnl_matrix_fixed< T, R, C > & | U () |
| Return the matrix U. | |
| vnl_matrix_fixed< T, R, C > const & | U () const |
| Return the matrix U. | |
| T | U (int i, int j) const |
| Return the matrix U's (i,j)th entry (to avoid svd.U()(i,j); ). | |
| vnl_diag_matrix_fixed < singval_t, C > & | W () |
| Get at DiagMatrix (q.v.) of singular values, sorted from largest to smallest. | |
| vnl_diag_matrix_fixed < singval_t, C > const & | W () const |
| Get at DiagMatrix (q.v.) of singular values, sorted from largest to smallest. | |
| vnl_diag_matrix_fixed < singval_t, C > & | Winverse () |
| vnl_diag_matrix_fixed < singval_t, C > const & | Winverse () const |
| singval_t & | W (int i, int j) |
| singval_t & | W (int i) |
| singval_t | sigma_max () const |
| singval_t | sigma_min () const |
| vnl_matrix_fixed< T, C, C > & | V () |
| Return the matrix V. | |
| vnl_matrix_fixed< T, C, C > const & | V () const |
| Return the matrix V. | |
| T | V (int i, int j) const |
| Return the matrix V's (i,j)th entry (to avoid svd.V()(i,j); ). | |
| vnl_matrix_fixed< T, C, R > | inverse () const |
| vnl_matrix_fixed< T, C, R > | pinverse (unsigned int rank=~0u) const |
| pseudo-inverse (for non-square matrix) of desired rank. | |
| vnl_matrix_fixed< T, R, C > | tinverse (unsigned int rank=~0u) const |
| Calculate inverse of transpose, using desired rank. | |
| vnl_matrix_fixed< T, R, C > | recompose (unsigned int rank=~0u) const |
| Recompose SVD to U*W*V', using desired rank. | |
| vnl_matrix< T > | solve (vnl_matrix< T > const &B) const |
| Solve the matrix equation M X = B, returning X. | |
| vnl_vector_fixed< T, C > | solve (vnl_vector_fixed< T, R > const &y) const |
| Solve the matrix-vector system M x = y, returning x. | |
| void | solve (T const *rhs, T *lhs) const |
| void | solve_preinverted (vnl_vector_fixed< T, R > const &rhs, vnl_vector_fixed< T, C > *out) const |
| Solve the matrix-vector system M x = y. | |
| vnl_matrix< T > | nullspace () const |
| Return N such that M * N = 0. | |
| vnl_matrix< T > | left_nullspace () const |
| Return N such that M' * N = 0. | |
| vnl_matrix< T > | nullspace (int required_nullspace_dimension) const |
| Return N such that M * N = 0. | |
| vnl_matrix< T > | left_nullspace (int required_nullspace_dimension) const |
| Implementation to be done yet; currently returns left_nullspace(). - PVR. | |
| vnl_vector_fixed< T, C > | nullvector () const |
| Return the rightmost column of V. | |
| vnl_vector_fixed< T, R > | left_nullvector () const |
| Return the rightmost column of U. | |
| bool | valid () const |
Private Member Functions | |
| vnl_svd_fixed (vnl_svd_fixed< T, R, C > const &) | |
| vnl_svd_fixed< T, R, C > & | operator= (vnl_svd_fixed< T, R, C > const &) |
Private Attributes | |
| vnl_matrix_fixed< T, R, C > | U_ |
| vnl_diag_matrix_fixed < singval_t, C > | W_ |
| vnl_diag_matrix_fixed < singval_t, C > | Winverse_ |
| vnl_matrix_fixed< T, C, C > | V_ |
| unsigned | rank_ |
| bool | have_max_ |
| singval_t | max_ |
| bool | have_min_ |
| singval_t | min_ |
| double | last_tol_ |
| bool | valid_ |
Detailed Description
template<class T, unsigned int R, unsigned int C>
class vnl_svd_fixed< T, R, C >
Holds the singular value decomposition of a vnl_matrix_fixed.
The class holds three matrices U, W, V such that the original matrix 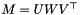 . The DiagMatrix W stores the singular values in decreasing order. The columns of U which correspond to the nonzero singular values form a basis for range of M, while the columns of V corresponding to the zero singular values are the nullspace.
. The DiagMatrix W stores the singular values in decreasing order. The columns of U which correspond to the nonzero singular values form a basis for range of M, while the columns of V corresponding to the zero singular values are the nullspace.
The SVD is computed at construction time, and inquiries may then be made of the SVD. In particular, this allows easy access to multiple right-hand-side solves without the bother of putting all the RHS's into a Matrix.
Definition at line 35 of file vnl_svd_fixed.h.
Member Typedef Documentation
| typedef vnl_numeric_traits<T>::abs_t vnl_svd_fixed< T, R, C >::singval_t |
The singular values of a matrix of complex<T> are of type T, not complex<T>.
Definition at line 39 of file vnl_svd_fixed.h.
Constructor & Destructor Documentation
| vnl_svd_fixed< T, R, C >::vnl_svd_fixed | ( | vnl_matrix_fixed< T, R, C > const & | M, |
| double | zero_out_tol = 0.0 |
||
| ) |
Construct a vnl_svd_fixed<T> object from 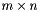 matrix
matrix 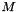 .
.
The vnl_svd_fixed<T> object contains matrices 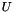 ,
, 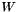 ,
, 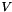 such that
such that 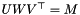 .
.
Uses linpack routine DSVDC to calculate an ``economy-size'' SVD where the returned 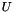 is the same size as
is the same size as 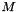 , while
, while 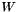 and
and 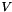 are both
are both 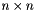 . This is efficient for large rectangular solves where
. This is efficient for large rectangular solves where 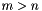 , typical in least squares.
, typical in least squares.
The optional argument zero_out_tol is used to mark the zero singular values: If nonnegative, any s.v. smaller than zero_out_tol in absolute value is set to zero. If zero_out_tol is negative, the zeroing is relative to |zero_out_tol| * sigma_max();
Definition at line 35 of file vnl_svd_fixed.txx.
| vnl_svd_fixed< T, R, C >::~vnl_svd_fixed | ( | ) | [inline] |
Definition at line 57 of file vnl_svd_fixed.h.
| vnl_svd_fixed< T, R, C >::vnl_svd_fixed | ( | vnl_svd_fixed< T, R, C > const & | ) | [inline, private] |
Definition at line 165 of file vnl_svd_fixed.h.
Member Function Documentation
| vnl_svd_fixed< T, R, C >::singval_t vnl_svd_fixed< T, R, C >::determinant_magnitude | ( | ) | const |
Calculate determinant as product of diagonals in W.
Definition at line 202 of file vnl_svd_fixed.txx.
| vnl_matrix_fixed<T,C,R> vnl_svd_fixed< T, R, C >::inverse | ( | ) | const [inline] |
Definition at line 105 of file vnl_svd_fixed.h.
| vnl_matrix< T > vnl_svd_fixed< T, R, C >::left_nullspace | ( | ) | const |
Return N such that M' * N = 0.
Return N s.t. M' * N = 0.
Definition at line 340 of file vnl_svd_fixed.txx.
| vnl_matrix< T > vnl_svd_fixed< T, R, C >::left_nullspace | ( | int | required_nullspace_dimension | ) | const |
Implementation to be done yet; currently returns left_nullspace(). - PVR.
- Todo:
- Implementation to be done yet; currently returns left_nullspace().
- PVr.
Definition at line 351 of file vnl_svd_fixed.txx.
| vnl_vector_fixed< T, R > vnl_svd_fixed< T, R, C >::left_nullvector | ( | ) | const |
Return the rightmost column of U.
Does not check to see whether or not the matrix actually was rank-deficient.
Definition at line 374 of file vnl_svd_fixed.txx.
| vnl_svd_fixed< T, R, C >::singval_t vnl_svd_fixed< T, R, C >::norm | ( | ) | const |
Definition at line 215 of file vnl_svd_fixed.txx.
| vnl_matrix< T > vnl_svd_fixed< T, R, C >::nullspace | ( | ) | const |
Return N such that M * N = 0.
Return N s.t. M * N = 0.
Definition at line 321 of file vnl_svd_fixed.txx.
| vnl_matrix< T > vnl_svd_fixed< T, R, C >::nullspace | ( | int | required_nullspace_dimension | ) | const |
Return N such that M * N = 0.
Return N s.t. M * N = 0.
Definition at line 332 of file vnl_svd_fixed.txx.
| vnl_vector_fixed< T, C > vnl_svd_fixed< T, R, C >::nullvector | ( | ) | const |
Return the rightmost column of V.
Does not check to see whether or not the matrix actually was rank-deficient - the caller is assumed to have examined W and decided that to his or her satisfaction.
Definition at line 362 of file vnl_svd_fixed.txx.
| vnl_svd_fixed<T,R,C>& vnl_svd_fixed< T, R, C >::operator= | ( | vnl_svd_fixed< T, R, C > const & | ) | [inline, private] |
Definition at line 166 of file vnl_svd_fixed.h.
| vnl_matrix_fixed< T, C, R > vnl_svd_fixed< T, R, C >::pinverse | ( | unsigned int | rank = ~0u | ) | const |
pseudo-inverse (for non-square matrix) of desired rank.
Calculate pseudo-inverse.
Definition at line 235 of file vnl_svd_fixed.txx.
| unsigned int vnl_svd_fixed< T, R, C >::rank | ( | ) | const [inline] |
Definition at line 67 of file vnl_svd_fixed.h.
| vnl_matrix_fixed< T, R, C > vnl_svd_fixed< T, R, C >::recompose | ( | unsigned int | rank = ~0u | ) | const |
Recompose SVD to U*W*V', using desired rank.
Recompose SVD to U*W*V'.
Definition at line 222 of file vnl_svd_fixed.txx.
| singval_t vnl_svd_fixed< T, R, C >::sigma_max | ( | ) | const [inline] |
Definition at line 92 of file vnl_svd_fixed.h.
| singval_t vnl_svd_fixed< T, R, C >::sigma_min | ( | ) | const [inline] |
Definition at line 93 of file vnl_svd_fixed.h.
| int vnl_svd_fixed< T, R, C >::singularities | ( | ) | const [inline] |
Definition at line 66 of file vnl_svd_fixed.h.
| vnl_matrix< T > vnl_svd_fixed< T, R, C >::solve | ( | vnl_matrix< T > const & | B | ) | const |
Solve the matrix equation M X = B, returning X.
Definition at line 261 of file vnl_svd_fixed.txx.
| vnl_vector_fixed< T, C > vnl_svd_fixed< T, R, C >::solve | ( | vnl_vector_fixed< T, R > const & | y | ) | const |
Solve the matrix-vector system M x = y, returning x.
Definition at line 284 of file vnl_svd_fixed.txx.
| void vnl_svd_fixed< T, R, C >::solve | ( | T const * | rhs, |
| T * | lhs | ||
| ) | const |
Definition at line 300 of file vnl_svd_fixed.txx.
| void vnl_svd_fixed< T, R, C >::solve_preinverted | ( | vnl_vector_fixed< T, R > const & | y, |
| vnl_vector_fixed< T, C > * | x_out | ||
| ) | const |
Solve the matrix-vector system M x = y.
Assuming that the singular values W have been preinverted by the caller.
Assume that the singular values W have been preinverted by the caller.
Definition at line 308 of file vnl_svd_fixed.txx.
| vnl_matrix_fixed< T, R, C > vnl_svd_fixed< T, R, C >::tinverse | ( | unsigned int | rank = ~0u | ) | const |
Calculate inverse of transpose, using desired rank.
Calculate (pseudo-)inverse of transpose.
Definition at line 248 of file vnl_svd_fixed.txx.
| vnl_matrix_fixed<T,R,C>& vnl_svd_fixed< T, R, C >::U | ( | ) | [inline] |
Return the matrix U.
Definition at line 75 of file vnl_svd_fixed.h.
| vnl_matrix_fixed<T,R,C> const& vnl_svd_fixed< T, R, C >::U | ( | ) | const [inline] |
Return the matrix U.
Definition at line 78 of file vnl_svd_fixed.h.
| T vnl_svd_fixed< T, R, C >::U | ( | int | i, |
| int | j | ||
| ) | const [inline] |
Return the matrix U's (i,j)th entry (to avoid svd.U()(i,j); ).
Definition at line 81 of file vnl_svd_fixed.h.
| vnl_matrix_fixed<T,C,C>& vnl_svd_fixed< T, R, C >::V | ( | ) | [inline] |
Return the matrix V.
Definition at line 96 of file vnl_svd_fixed.h.
| vnl_matrix_fixed<T,C,C> const& vnl_svd_fixed< T, R, C >::V | ( | ) | const [inline] |
Return the matrix V.
Definition at line 99 of file vnl_svd_fixed.h.
| T vnl_svd_fixed< T, R, C >::V | ( | int | i, |
| int | j | ||
| ) | const [inline] |
Return the matrix V's (i,j)th entry (to avoid svd.V()(i,j); ).
Definition at line 102 of file vnl_svd_fixed.h.
| bool vnl_svd_fixed< T, R, C >::valid | ( | ) | const [inline] |
Definition at line 148 of file vnl_svd_fixed.h.
| vnl_diag_matrix_fixed<singval_t, C>& vnl_svd_fixed< T, R, C >::W | ( | ) | [inline] |
Get at DiagMatrix (q.v.) of singular values, sorted from largest to smallest.
Definition at line 84 of file vnl_svd_fixed.h.
| vnl_diag_matrix_fixed<singval_t, C> const& vnl_svd_fixed< T, R, C >::W | ( | ) | const [inline] |
Get at DiagMatrix (q.v.) of singular values, sorted from largest to smallest.
Definition at line 87 of file vnl_svd_fixed.h.
| singval_t& vnl_svd_fixed< T, R, C >::W | ( | int | i, |
| int | j | ||
| ) | [inline] |
Definition at line 90 of file vnl_svd_fixed.h.
| singval_t& vnl_svd_fixed< T, R, C >::W | ( | int | i | ) | [inline] |
Definition at line 91 of file vnl_svd_fixed.h.
| singval_t vnl_svd_fixed< T, R, C >::well_condition | ( | ) | const [inline] |
Definition at line 68 of file vnl_svd_fixed.h.
| vnl_diag_matrix_fixed<singval_t, C>& vnl_svd_fixed< T, R, C >::Winverse | ( | ) | [inline] |
Definition at line 88 of file vnl_svd_fixed.h.
| vnl_diag_matrix_fixed<singval_t, C> const& vnl_svd_fixed< T, R, C >::Winverse | ( | ) | const [inline] |
Definition at line 89 of file vnl_svd_fixed.h.
| void vnl_svd_fixed< T, R, C >::zero_out_absolute | ( | double | tol = 1e-8 | ) |
find weights below threshold tol, zero them out, and update W_ and Winverse_.
Definition at line 170 of file vnl_svd_fixed.txx.
| void vnl_svd_fixed< T, R, C >::zero_out_relative | ( | double | tol = 1e-8 | ) |
find weights below tol*max(w) and zero them out.
Definition at line 192 of file vnl_svd_fixed.txx.
Member Data Documentation
bool vnl_svd_fixed< T, R, C >::have_max_ [private] |
Definition at line 157 of file vnl_svd_fixed.h.
bool vnl_svd_fixed< T, R, C >::have_min_ [private] |
Definition at line 159 of file vnl_svd_fixed.h.
double vnl_svd_fixed< T, R, C >::last_tol_ [private] |
Definition at line 161 of file vnl_svd_fixed.h.
singval_t vnl_svd_fixed< T, R, C >::max_ [private] |
Definition at line 158 of file vnl_svd_fixed.h.
singval_t vnl_svd_fixed< T, R, C >::min_ [private] |
Definition at line 160 of file vnl_svd_fixed.h.
unsigned vnl_svd_fixed< T, R, C >::rank_ [private] |
Definition at line 156 of file vnl_svd_fixed.h.
vnl_matrix_fixed<T, R, C> vnl_svd_fixed< T, R, C >::U_ [private] |
Definition at line 152 of file vnl_svd_fixed.h.
vnl_matrix_fixed<T, C, C> vnl_svd_fixed< T, R, C >::V_ [private] |
Definition at line 155 of file vnl_svd_fixed.h.
bool vnl_svd_fixed< T, R, C >::valid_ [private] |
Definition at line 162 of file vnl_svd_fixed.h.
vnl_diag_matrix_fixed<singval_t, C> vnl_svd_fixed< T, R, C >::W_ [private] |
Definition at line 153 of file vnl_svd_fixed.h.
vnl_diag_matrix_fixed<singval_t, C> vnl_svd_fixed< T, R, C >::Winverse_ [private] |
Definition at line 154 of file vnl_svd_fixed.h.
The documentation for this class was generated from the following files:
- core/vnl/algo/vnl_svd_fixed.h
- core/vnl/algo/vnl_svd_fixed.txx
 1.7.5.1
1.7.5.1