Holds the singular value decomposition of a vnl_matrix. More...
#include <vnl_svd.h>
Public Types | |
| typedef vnl_numeric_traits< T > ::abs_t | singval_t |
| The singular values of a matrix of complex<T> are of type T, not complex<T>. | |
Public Member Functions | |
| vnl_svd (vnl_matrix< T > const &M, double zero_out_tol=0.0) | |
Construct a vnl_svd<T> object from 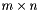 matrix matrix 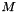 . . | |
| ~vnl_svd () | |
| void | zero_out_absolute (double tol=1e-8) |
| find weights below threshold tol, zero them out, and update W_ and Winverse_. | |
| void | zero_out_relative (double tol=1e-8) |
| find weights below tol*max(w) and zero them out. | |
| int | singularities () const |
| unsigned int | rank () const |
| singval_t | well_condition () const |
| singval_t | determinant_magnitude () const |
| Calculate determinant as product of diagonals in W. | |
| singval_t | norm () const |
| vnl_matrix< T > & | U () |
| Return the matrix U. | |
| vnl_matrix< T > const & | U () const |
| Return the matrix U. | |
| T | U (int i, int j) const |
| Return the matrix U's (i,j)th entry (to avoid svd.U()(i,j); ). | |
| vnl_diag_matrix< singval_t > & | W () |
| Get at DiagMatrix (q.v.) of singular values, sorted from largest to smallest. | |
| vnl_diag_matrix< singval_t > const & | W () const |
| Get at DiagMatrix (q.v.) of singular values, sorted from largest to smallest. | |
| vnl_diag_matrix< singval_t > & | Winverse () |
| vnl_diag_matrix< singval_t > const & | Winverse () const |
| singval_t & | W (int i, int j) |
| singval_t & | W (int i) |
| singval_t | sigma_max () const |
| singval_t | sigma_min () const |
| vnl_matrix< T > & | V () |
| Return the matrix V. | |
| vnl_matrix< T > const & | V () const |
| Return the matrix V. | |
| T | V (int i, int j) const |
| Return the matrix V's (i,j)th entry (to avoid svd.V()(i,j); ). | |
| vnl_matrix< T > | inverse () const |
| vnl_matrix< T > | pinverse (unsigned int rank=~0u) const |
| pseudo-inverse (for non-square matrix) of desired rank. | |
| vnl_matrix< T > | tinverse (unsigned int rank=~0u) const |
| Calculate inverse of transpose, using desired rank. | |
| vnl_matrix< T > | recompose (unsigned int rank=~0u) const |
| Recompose SVD to U*W*V', using desired rank. | |
| vnl_matrix< T > | solve (vnl_matrix< T > const &B) const |
| Solve the matrix equation M X = B, returning X. | |
| vnl_vector< T > | solve (vnl_vector< T > const &y) const |
| Solve the matrix-vector system M x = y, returning x. | |
| void | solve (T const *rhs, T *lhs) const |
| void | solve_preinverted (vnl_vector< T > const &rhs, vnl_vector< T > *out) const |
| Solve the matrix-vector system M x = y. | |
| vnl_matrix< T > | nullspace () const |
| Return N such that M * N = 0. | |
| vnl_matrix< T > | left_nullspace () const |
| Return N such that M' * N = 0. | |
| vnl_matrix< T > | nullspace (int required_nullspace_dimension) const |
| Return N such that M * N = 0. | |
| vnl_matrix< T > | left_nullspace (int required_nullspace_dimension) const |
| Implementation to be done yet; currently returns left_nullspace(). - PVR. | |
| vnl_vector< T > | nullvector () const |
| Return the rightmost column of V. | |
| vnl_vector< T > | left_nullvector () const |
| Return the rightmost column of U. | |
| bool | valid () const |
Private Member Functions | |
| vnl_svd (vnl_svd< T > const &) | |
| vnl_svd< T > & | operator= (vnl_svd< T > const &) |
Private Attributes | |
| int | m_ |
| int | n_ |
| vnl_matrix< T > | U_ |
| vnl_diag_matrix< singval_t > | W_ |
| vnl_diag_matrix< singval_t > | Winverse_ |
| vnl_matrix< T > | V_ |
| unsigned | rank_ |
| bool | have_max_ |
| singval_t | max_ |
| bool | have_min_ |
| singval_t | min_ |
| double | last_tol_ |
| bool | valid_ |
Detailed Description
template<class T>
class vnl_svd< T >
Holds the singular value decomposition of a vnl_matrix.
The class holds three matrices U, W, V such that the original matrix 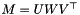 . The DiagMatrix W stores the singular values in decreasing order. The columns of U which correspond to the nonzero singular values form a basis for range of M, while the columns of V corresponding to the zero singular values are the nullspace.
. The DiagMatrix W stores the singular values in decreasing order. The columns of U which correspond to the nonzero singular values form a basis for range of M, while the columns of V corresponding to the zero singular values are the nullspace.
The SVD is computed at construction time, and inquiries may then be made of the SVD. In particular, this allows easy access to multiple right-hand-side solves without the bother of putting all the RHS's into a Matrix.
This class is supplied even though there is an existing vnl_matrix method for several reasons:
It is more convenient to use as it manages all the storage for the U,S,V matrices, allowing repeated queries of the same SVD results.
It avoids namespace clutter in the Matrix class. While svd() is a perfectly reasonable method for a Matrix, there are many other decompositions that might be of interest, and adding them all would make for a very large Matrix class.
It demonstrates the holder model of compute class, implementing an algorithm on an object without adding a member that may not be of general interest. A similar pattern can be used for other decompositions which are not defined as members of the library Matrix class.
It extends readily to n-ary operations, such as generalized eigensystems, which cannot be members of just one matrix.
Member Typedef Documentation
Constructor & Destructor Documentation
| vnl_svd< T >::vnl_svd | ( | vnl_matrix< T > const & | M, |
| double | zero_out_tol = 0.0 |
||
| ) |
Construct a vnl_svd<T> object from 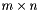 matrix
matrix 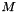 .
.
The vnl_svd<T> object contains matrices 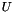 ,
, 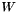 ,
, 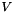 such that
such that 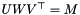 .
.
Uses linpack routine DSVDC to calculate an ``economy-size'' SVD where the returned 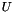 is the same size as
is the same size as 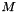 , while
, while 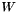 and
and 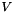 are both
are both 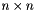 . This is efficient for large rectangular solves where
. This is efficient for large rectangular solves where 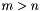 , typical in least squares.
, typical in least squares.
The optional argument zero_out_tol is used to mark the zero singular values: If nonnegative, any s.v. smaller than zero_out_tol in absolute value is set to zero. If zero_out_tol is negative, the zeroing is relative to |zero_out_tol| * sigma_max();
Definition at line 35 of file vnl_svd.txx.
Member Function Documentation
Calculate determinant as product of diagonals in W.
Definition at line 210 of file vnl_svd.txx.
| vnl_matrix<T> vnl_svd< T >::inverse | ( | ) | const [inline] |
| vnl_matrix< T > vnl_svd< T >::left_nullspace | ( | ) | const |
Return N such that M' * N = 0.
Return N s.t. M' * N = 0.
Definition at line 381 of file vnl_svd.txx.
| vnl_matrix< T > vnl_svd< T >::left_nullspace | ( | int | required_nullspace_dimension | ) | const |
Implementation to be done yet; currently returns left_nullspace(). - PVR.
- Todo:
- Implementation to be done yet; currently returns left_nullspace().
- PVr.
Definition at line 392 of file vnl_svd.txx.
| vnl_vector< T > vnl_svd< T >::left_nullvector | ( | ) | const |
Return the rightmost column of U.
Does not check to see whether or not the matrix actually was rank-deficient.
Definition at line 415 of file vnl_svd.txx.
Definition at line 223 of file vnl_svd.txx.
| vnl_matrix< T > vnl_svd< T >::nullspace | ( | ) | const |
| vnl_matrix< T > vnl_svd< T >::nullspace | ( | int | required_nullspace_dimension | ) | const |
| vnl_vector< T > vnl_svd< T >::nullvector | ( | ) | const |
Return the rightmost column of V.
Does not check to see whether or not the matrix actually was rank-deficient - the caller is assumed to have examined W and decided that to his or her satisfaction.
Definition at line 403 of file vnl_svd.txx.
| vnl_matrix< T > vnl_svd< T >::pinverse | ( | unsigned int | rank = ~0u | ) | const |
pseudo-inverse (for non-square matrix) of desired rank.
Calculate pseudo-inverse.
Definition at line 244 of file vnl_svd.txx.
| unsigned int vnl_svd< T >::rank | ( | ) | const [inline] |
| vnl_matrix< T > vnl_svd< T >::recompose | ( | unsigned int | rank = ~0u | ) | const |
Recompose SVD to U*W*V', using desired rank.
Recompose SVD to U*W*V'.
Definition at line 230 of file vnl_svd.txx.
| int vnl_svd< T >::singularities | ( | ) | const [inline] |
| vnl_matrix< T > vnl_svd< T >::solve | ( | vnl_matrix< T > const & | B | ) | const |
Solve the matrix equation M X = B, returning X.
Definition at line 272 of file vnl_svd.txx.
| vnl_vector< T > vnl_svd< T >::solve | ( | vnl_vector< T > const & | y | ) | const |
Solve the matrix-vector system M x = y, returning x.
Definition at line 295 of file vnl_svd.txx.
| void vnl_svd< T >::solve | ( | T const * | rhs, |
| T * | lhs | ||
| ) | const |
Definition at line 334 of file vnl_svd.txx.
| void vnl_svd< T >::solve_preinverted | ( | vnl_vector< T > const & | y, |
| vnl_vector< T > * | x_out | ||
| ) | const |
Solve the matrix-vector system M x = y.
Assuming that the singular values W have been preinverted by the caller.
Assume that the singular values W have been preinverted by the caller.
Definition at line 342 of file vnl_svd.txx.
| vnl_matrix< T > vnl_svd< T >::tinverse | ( | unsigned int | rank = ~0u | ) | const |
Calculate inverse of transpose, using desired rank.
Calculate (pseudo-)inverse of transpose.
Definition at line 258 of file vnl_svd.txx.
| vnl_matrix<T>& vnl_svd< T >::U | ( | ) | [inline] |
| vnl_matrix<T> const& vnl_svd< T >::U | ( | ) | const [inline] |
| T vnl_svd< T >::U | ( | int | i, |
| int | j | ||
| ) | const [inline] |
| vnl_matrix<T>& vnl_svd< T >::V | ( | ) | [inline] |
| vnl_matrix<T> const& vnl_svd< T >::V | ( | ) | const [inline] |
| T vnl_svd< T >::V | ( | int | i, |
| int | j | ||
| ) | const [inline] |
| bool vnl_svd< T >::valid | ( | ) | const [inline] |
| vnl_diag_matrix<singval_t>& vnl_svd< T >::W | ( | ) | [inline] |
| vnl_diag_matrix<singval_t> const& vnl_svd< T >::W | ( | ) | const [inline] |
| vnl_diag_matrix<singval_t>& vnl_svd< T >::Winverse | ( | ) | [inline] |
| vnl_diag_matrix<singval_t> const& vnl_svd< T >::Winverse | ( | ) | const [inline] |
| void vnl_svd< T >::zero_out_absolute | ( | double | tol = 1e-8 | ) |
find weights below threshold tol, zero them out, and update W_ and Winverse_.
Definition at line 179 of file vnl_svd.txx.
| void vnl_svd< T >::zero_out_relative | ( | double | tol = 1e-8 | ) |
find weights below tol*max(w) and zero them out.
Definition at line 200 of file vnl_svd.txx.
Member Data Documentation
vnl_matrix<T> vnl_svd< T >::U_ [private] |
vnl_matrix<T> vnl_svd< T >::V_ [private] |
vnl_diag_matrix<singval_t> vnl_svd< T >::W_ [private] |
vnl_diag_matrix<singval_t> vnl_svd< T >::Winverse_ [private] |
The documentation for this class was generated from the following files:
- core/vnl/algo/vnl_svd.h
- core/vnl/algo/vnl_svd.txx
 1.7.5.1
1.7.5.1