Find the eigenvalues of a sparse symmetric matrix. More...
#include <vnl_sparse_symmetric_eigensystem.h>
Public Member Functions | |
| vnl_sparse_symmetric_eigensystem () | |
| ~vnl_sparse_symmetric_eigensystem () | |
| int | CalculateNPairs (vnl_sparse_matrix< double > &M, int n, bool smallest=true, long nfigures=10) |
| Here is where the fortran converted code gets called. | |
| int | CalculateNPairs (vnl_sparse_matrix< double > &A, vnl_sparse_matrix< double > &B, int nEV, double tolerance=0, int numberLanczosVecs=0, bool smallest=false, bool magnitude=true, int maxIterations=0, double sigma=0.0) |
| Here is where the fortran converted code gets called. | |
| vnl_vector< double > | get_eigenvector (int i) const |
| Return a calculated eigenvector. | |
| double | get_eigenvalue (int i) const |
| int | CalculateProduct (int n, int m, const double *p, double *q) |
| Callback from solver to calculate the product A p. | |
| int | SaveVectors (int n, int m, const double *q, int base) |
| Callback to store vectors for dnlaso. | |
| int | RestoreVectors (int n, int m, double *q, int base) |
| Callback to restore vectors for dnlaso. | |
Protected Attributes | |
| int | nvalues |
| vnl_vector< double > * | vectors |
| double * | values |
| vnl_sparse_matrix< double > * | mat |
| vnl_sparse_matrix< double > * | Bmat |
| vcl_vector< double * > | temp_store |
Detailed Description
Find the eigenvalues of a sparse symmetric matrix.
Solve the standard eigenproblem 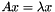 , or the generalized eigenproblem of
, or the generalized eigenproblem of 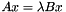 , where
, where 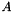 symmetric and sparse and, optionally, B sparse, symmetric, and positive definite. The block Lanczos algorithm is used to allow the recovery of a number of eigenvalue/eigenvector pairs from either end of the spectrum, to a required accuracy.
symmetric and sparse and, optionally, B sparse, symmetric, and positive definite. The block Lanczos algorithm is used to allow the recovery of a number of eigenvalue/eigenvector pairs from either end of the spectrum, to a required accuracy.
Uses the dnlaso routine from the LASO package of netlib for solving the standard case. Uses the dsaupd routine from the ARPACK package of netlib for solving the generalized case.
Definition at line 36 of file vnl_sparse_symmetric_eigensystem.h.
Constructor & Destructor Documentation
| vnl_sparse_symmetric_eigensystem::vnl_sparse_symmetric_eigensystem | ( | ) |
Definition at line 62 of file vnl_sparse_symmetric_eigensystem.cxx.
| vnl_sparse_symmetric_eigensystem::~vnl_sparse_symmetric_eigensystem | ( | ) |
Definition at line 67 of file vnl_sparse_symmetric_eigensystem.cxx.
Member Function Documentation
| int vnl_sparse_symmetric_eigensystem::CalculateNPairs | ( | vnl_sparse_matrix< double > & | M, |
| int | n, | ||
| bool | smallest = true, |
||
| long | nfigures = 10 |
||
| ) |
Here is where the fortran converted code gets called.
The sparse matrix M is assumed to be symmetric. The n smallest eigenvalues and their corresponding eigenvectors are calculated if smallest is true (the default). Otherwise the n largest eigenpairs are found. The accuracy of the eigenvalues is to nfigures decimal digits. Returns 0 if successful, non-zero otherwise.
Definition at line 83 of file vnl_sparse_symmetric_eigensystem.cxx.
| int vnl_sparse_symmetric_eigensystem::CalculateNPairs | ( | vnl_sparse_matrix< double > & | A, |
| vnl_sparse_matrix< double > & | B, | ||
| int | nEV, | ||
| double | tolerance = 0, |
||
| int | numberLanczosVecs = 0, |
||
| bool | smallest = false, |
||
| bool | magnitude = true, |
||
| int | maxIterations = 0, |
||
| double | sigma = 0.0 |
||
| ) |
Here is where the fortran converted code gets called.
The sparse matrix A is assumed to be symmetric. Find n eigenvalue/eigenvectors of the eigenproblem A * x = lambda * B * x. !smallest and !magnitude - compute the N largest (algebraic) eigenvalues smallest and !magnitude - compute the N smallest (algebraic) eigenvalues !smallest and magnitude - compute the N largest (magnitude) eigenvalues smallest and magnitude - compute the nev smallest (magnitude) eigenvalues set sigma for shift/invert mode
Definition at line 217 of file vnl_sparse_symmetric_eigensystem.cxx.
| int vnl_sparse_symmetric_eigensystem::CalculateProduct | ( | int | n, |
| int | m, | ||
| const double * | p, | ||
| double * | q | ||
| ) |
Callback from solver to calculate the product A p.
Definition at line 457 of file vnl_sparse_symmetric_eigensystem.cxx.
| double vnl_sparse_symmetric_eigensystem::get_eigenvalue | ( | int | i | ) | const |
Definition at line 522 of file vnl_sparse_symmetric_eigensystem.cxx.
| vnl_vector< double > vnl_sparse_symmetric_eigensystem::get_eigenvector | ( | int | i | ) | const |
Return a calculated eigenvector.
Definition at line 516 of file vnl_sparse_symmetric_eigensystem.cxx.
| int vnl_sparse_symmetric_eigensystem::RestoreVectors | ( | int | n, |
| int | m, | ||
| double * | q, | ||
| int | base | ||
| ) |
Callback to restore vectors for dnlaso.
Definition at line 494 of file vnl_sparse_symmetric_eigensystem.cxx.
| int vnl_sparse_symmetric_eigensystem::SaveVectors | ( | int | n, |
| int | m, | ||
| const double * | q, | ||
| int | base | ||
| ) |
Callback to store vectors for dnlaso.
Definition at line 469 of file vnl_sparse_symmetric_eigensystem.cxx.
Member Data Documentation
vnl_sparse_matrix<double>* vnl_sparse_symmetric_eigensystem::Bmat [protected] |
Definition at line 78 of file vnl_sparse_symmetric_eigensystem.h.
vnl_sparse_matrix<double>* vnl_sparse_symmetric_eigensystem::mat [protected] |
Definition at line 76 of file vnl_sparse_symmetric_eigensystem.h.
int vnl_sparse_symmetric_eigensystem::nvalues [protected] |
Definition at line 71 of file vnl_sparse_symmetric_eigensystem.h.
vcl_vector<double*> vnl_sparse_symmetric_eigensystem::temp_store [protected] |
Definition at line 80 of file vnl_sparse_symmetric_eigensystem.h.
double* vnl_sparse_symmetric_eigensystem::values [protected] |
Definition at line 73 of file vnl_sparse_symmetric_eigensystem.h.
vnl_vector<double>* vnl_sparse_symmetric_eigensystem::vectors [protected] |
Definition at line 72 of file vnl_sparse_symmetric_eigensystem.h.
The documentation for this class was generated from the following files:
- core/vnl/algo/vnl_sparse_symmetric_eigensystem.h
- core/vnl/algo/vnl_sparse_symmetric_eigensystem.cxx
 1.7.5.1
1.7.5.1