Evaluation of real polynomials at real and complex points. More...

#include <vnl_real_polynomial.h>

Public Member Functions
	vnl_real_polynomial (vnl_vector< double > const &a)
	Initialize polynomial.
	vnl_real_polynomial (double const *a, unsigned len)
	Initialize polynomial from C vector.
	vnl_real_polynomial (double a)
	Initialize polynomial from double.
	vnl_real_polynomial (int d)
	Initialize polynomial of a given degree.
bool	operator== (vnl_real_polynomial const &p) const
	comparison operator.
double	evaluate (double x) const
	Evaluate polynomial at value x.
double	evaluate_integral (double x) const
	Evaluate integral at x (assuming constant of integration is zero).
double	evaluate_integral (double x1, double x2) const
	Evaluate integral between x1 and x2.
double	devaluate (double x) const
	Evaluate derivative at value x.
vcl_complex< double >	evaluate (vcl_complex< double > const &x) const
	Evaluate polynomial at complex value x.
vcl_complex< double >	devaluate (vcl_complex< double > const &x) const
	Evaluate derivative at complex value x.
vnl_real_polynomial	derivative () const
	Return derivative of this polynomial.
vnl_real_polynomial	primitive () const
	Return primitive function (inverse derivative) of this polynomial.
vnl_real_polynomial &	operator+= (vnl_real_polynomial const &rhs)
	Add rhs to this and return *this.
vnl_real_polynomial &	operator-= (vnl_real_polynomial const &rhs)
	Subtract rhs from this and return *this.
vnl_real_polynomial &	operator*= (vnl_real_polynomial const &rhs)
	Multiply rhs with this and return *this.
int	degree () const
	Return the degree (highest power of x) of the polynomial.
double &	operator[] (int i)
	Access to the polynomial coefficients.
double	operator[] (int i) const
	Access to the polynomial coefficients.
const vnl_vector< double > &	coefficients () const
	Return the vector of coefficients.
vnl_vector< double > &	coefficients ()
	Return the vector of coefficients.
void	set_coefficients (vnl_vector< double > const &coeffs)
void	print (vcl_ostream &os) const
	Print this polynomial to stream.
Protected Attributes
vnl_vector< double >	coeffs_
	The coefficients of the polynomial.
Related Functions
(Note that these are not member functions.)
void	vsl_b_write (vsl_b_ostream &os, const vnl_real_polynomial &v)
	Binary save vnl_real_polynomial to stream.
void	vsl_b_read (vsl_b_istream &is, vnl_real_polynomial &v)
	Binary load vnl_real_polynomial from stream.
void	vsl_print_summary (vcl_ostream &os, const vnl_real_polynomial &b)
	Print human readable summary of object to a stream.
vnl_real_polynomial	operator+ (const vnl_real_polynomial &f1, const vnl_real_polynomial &f2)
	Returns polynomial which is sum of two polynomials f1(x)+f2(x).
vnl_real_polynomial	operator- (const vnl_real_polynomial &f1, const vnl_real_polynomial &f2)
	Returns polynomial which is different of two polynomials f1(x)-f2(x).
double	vnl_rms_difference (const vnl_real_polynomial &f1, const vnl_real_polynomial &f2, double x1, double x2)
	Returns RMS difference between f1 and f2 over range [x1,x2].

Detailed Description

Evaluation of real polynomials at real and complex points.

vnl_real_polynomial represents a univariate polynomial with real coefficients, stored as a vector of doubles. This allows evaluation of the polynomial 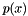$p(x)$ at given values of 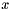$x$ , or of its derivative $p'(x)$ .

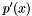The coefficients (coeffs_) are stored as a vnl_vector, where coeffs_[n] is the coefficient of the x^(d-n) term, where d is the degree of the polynomial. Otherwise said, the coefficients are stored starting with the highest degree term.

Roots may be extracted using the roots() method.

Definition at line 39 of file vnl_real_polynomial.h.

Constructor & Destructor Documentation

vnl_real_polynomial::vnl_real_polynomial ( vnl_vector< double > const & a ) [inline]

Initialize polynomial.

The polynomial is $a[0] x^d + a[1] x^{d-1} + \cdots + a[d] = 0$ .

Definition at line 44 of file vnl_real_polynomial.h.

vnl_real_polynomial::vnl_real_polynomial	(	double const *	a,
		unsigned	len
	)		`[inline]`

Initialize polynomial from C vector.

The parameter len is the number of coefficients, one greater than the degree.

Definition at line 51 of file vnl_real_polynomial.h.

vnl_real_polynomial::vnl_real_polynomial ( double a ) [inline]

Initialize polynomial from double.

Useful when adding or multiplying a polynomial and a number.

Definition at line 57 of file vnl_real_polynomial.h.

vnl_real_polynomial::vnl_real_polynomial ( int d ) [inline]

Initialize polynomial of a given degree.

Definition at line 60 of file vnl_real_polynomial.h.

Member Function Documentation

const vnl_vector<double>& vnl_real_polynomial::coefficients ( ) const [inline]

Return the vector of coefficients.

Definition at line 111 of file vnl_real_polynomial.h.

vnl_vector<double>& vnl_real_polynomial::coefficients ( ) [inline]

Return the vector of coefficients.

Definition at line 113 of file vnl_real_polynomial.h.

int vnl_real_polynomial::degree ( ) const [inline]

Return the degree (highest power of x) of the polynomial.

Definition at line 103 of file vnl_real_polynomial.h.

vnl_real_polynomial vnl_real_polynomial::derivative ( ) const

Return derivative of this polynomial.

Definition at line 193 of file vnl_real_polynomial.cxx.

double vnl_real_polynomial::devaluate ( double x ) const

Evaluate derivative at value x.

Definition at line 64 of file vnl_real_polynomial.cxx.

vcl_complex< double > vnl_real_polynomial::devaluate ( vcl_complex< double > const & x ) const

Evaluate derivative at complex value x.

Evaluate derivative at complex value x. Not implemented.

Definition at line 71 of file vnl_real_polynomial.cxx.

double vnl_real_polynomial::evaluate ( double x ) const

Evaluate polynomial at value x.

vcl_complex<double> vnl_real_polynomial::evaluate ( vcl_complex< double > const & x ) const

Evaluate polynomial at complex value x.

double vnl_real_polynomial::evaluate_integral ( double x ) const

Evaluate integral at x (assuming constant of integration is zero).

Definition at line 77 of file vnl_real_polynomial.cxx.

double vnl_real_polynomial::evaluate_integral	(	double	x1,
		double	x2
	)		const

Evaluate integral between x1 and x2.

Definition at line 95 of file vnl_real_polynomial.cxx.

vnl_real_polynomial & vnl_real_polynomial::operator*= ( vnl_real_polynomial const & rhs )

Multiply rhs with this and return *this.

multiply rhs with this and return *this.

Definition at line 173 of file vnl_real_polynomial.cxx.

vnl_real_polynomial & vnl_real_polynomial::operator+= ( vnl_real_polynomial const & rhs )

Add rhs to this and return *this.

Definition at line 161 of file vnl_real_polynomial.cxx.

vnl_real_polynomial & vnl_real_polynomial::operator-= ( vnl_real_polynomial const & rhs )

Subtract rhs from this and return *this.

Definition at line 167 of file vnl_real_polynomial.cxx.

bool vnl_real_polynomial::operator== ( vnl_real_polynomial const & p ) const [inline]

comparison operator.

Definition at line 63 of file vnl_real_polynomial.h.

double& vnl_real_polynomial::operator[] ( int i ) [inline]

Access to the polynomial coefficients.

Definition at line 106 of file vnl_real_polynomial.h.

double vnl_real_polynomial::operator[] ( int i ) const [inline]

Access to the polynomial coefficients.

Definition at line 108 of file vnl_real_polynomial.h.

vnl_real_polynomial vnl_real_polynomial::primitive ( ) const

Return primitive function (inverse derivative) of this polynomial.

Since a primitive function is not unique, the one with constant = 0 is returned

Definition at line 204 of file vnl_real_polynomial.cxx.

void vnl_real_polynomial::print ( vcl_ostream & os ) const

Print this polynomial to stream.

Definition at line 214 of file vnl_real_polynomial.cxx.

void vnl_real_polynomial::set_coefficients ( vnl_vector< double > const & coeffs ) [inline]

Definition at line 115 of file vnl_real_polynomial.h.

Friends And Related Function Documentation

vnl_real_polynomial operator+	(	const vnl_real_polynomial &	f1,
		const vnl_real_polynomial &	f2
	)		`[related]`

Returns polynomial which is sum of two polynomials f1(x)+f2(x).

Definition at line 101 of file vnl_real_polynomial.cxx.

vnl_real_polynomial operator-	(	const vnl_real_polynomial &	f1,
		const vnl_real_polynomial &	f2
	)		`[related]`

Returns polynomial which is different of two polynomials f1(x)-f2(x).

Definition at line 123 of file vnl_real_polynomial.cxx.

double vnl_rms_difference	(	const vnl_real_polynomial &	f1,
		const vnl_real_polynomial &	f2,
		double	x1,
		double	x2
	)		`[related]`

Returns RMS difference between f1 and f2 over range [x1,x2].

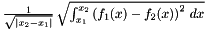
$\frac1{\sqrt{|x_2-x_1|}}\,\sqrt{\int_{x_1}^{x_2}\left(f_1(x)-f_2(x)\right)^2\,dx}$

Definition at line 180 of file vnl_real_polynomial.cxx.

void vsl_b_read	(	vsl_b_istream &	is,
		vnl_real_polynomial &	v
	)		`[related]`

Binary load vnl_real_polynomial from stream.

Definition at line 26 of file vnl_io_real_polynomial.cxx.

void vsl_b_write	(	vsl_b_ostream &	os,
		const vnl_real_polynomial &	v
	)		`[related]`

Binary save vnl_real_polynomial to stream.

Definition at line 16 of file vnl_io_real_polynomial.cxx.

void vsl_print_summary	(	vcl_ostream &	os,
		const vnl_real_polynomial &	b
	)		`[related]`

Print human readable summary of object to a stream.

Definition at line 50 of file vnl_io_real_polynomial.cxx.

Member Data Documentation

vnl_vector<double> vnl_real_polynomial::coeffs_ [protected]

The coefficients of the polynomial.

coeffs_.back() is the const term. coeffs_[n] is the coefficient of the x^(d-n) term, where d=coeffs_.size()-1

Invariant:: coeffs_size() >= 1;

Definition at line 126 of file vnl_real_polynomial.h.

The documentation for this class was generated from the following files:

Public Member Functions

Protected Attributes

Related Functions

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

Member Data Documentation