Evaluation of polynomials. More...
#include <vnl_polynomial.h>
Public Member Functions | |
| vnl_polynomial (vcl_vector< T > const &a) | |
| Initialize the polynomial from its coefficients, lowest order first. | |
| vnl_polynomial (T const *a, unsigned len) | |
| Initialize polynomial from C array, highest order first. | |
| vnl_polynomial (T const &a) | |
| Initialize polynomial from single value, thus creating a monomial. | |
| vnl_polynomial (int d=-1) | |
| Initialize polynomial of a given degree. | |
| bool | operator== (vnl_polynomial< T > const &p) const |
| comparison operator. | |
| vnl_polynomial< T > | operator- () const |
| Returns negative of this polynomial. | |
| vnl_polynomial< T > | operator+ (vnl_polynomial< T > const &f) const |
| Returns polynomial which is sum of this with polynomial f. | |
| vnl_polynomial< T > | operator- (vnl_polynomial< T > const &f) const |
| Returns polynomial which is difference of this with polynomial f. | |
| vnl_polynomial< T > | operator* (vnl_polynomial< T > const &f) const |
| Returns polynomial which is product of this with polynomial f. | |
| vnl_polynomial< T > | operator/ (vnl_polynomial< T > const &f) const |
| Returns polynomial which is the result of the long division by polynomial f. | |
| vnl_polynomial< T > | operator% (vnl_polynomial< T > const &f) const |
| Returns polynomial which is the remainder after a long division by polynomial f. | |
| vnl_polynomial< T > & | operator+= (vnl_polynomial< T > const &f) |
| vnl_polynomial< T > & | operator-= (vnl_polynomial< T > const &f) |
| vnl_polynomial< T > & | operator*= (vnl_polynomial< T > const &f) |
| vnl_polynomial< T > & | operator/= (vnl_polynomial< T > const &f) |
| vnl_polynomial< T > & | operator%= (vnl_polynomial< T > const &f) |
| T | evaluate (T const &x) const |
Evaluate polynomial at value x. | |
| vnl_polynomial< T > | derivative () const |
| Return derivative of this polynomial. | |
| T | devaluate (T const &x) const |
Evaluate derivative at value x. | |
| vnl_polynomial< T > | primitive () const |
| Return primitive function (inverse derivative) of this polynomial. | |
| T | evaluate_integral (T const &x) const |
Evaluate integral at x (assuming constant of integration is zero). | |
| T | evaluate_integral (T const &x1, T const &x2) const |
Evaluate integral between x1 and x2. | |
| int | degree () const |
| Return the degree (highest power of X) of the polynomial. | |
| T & | operator[] (unsigned int i) |
| Access to the polynomial coefficient of $X^i$. | |
| T | operator[] (unsigned int i) const |
| Access to the polynomial coefficient of $X^i$. | |
| const vcl_vector< T > & | coefficients () const |
| Return the vector of coefficients. | |
| vcl_vector< T > & | coefficients () |
| Return the vector of coefficients. | |
| void | set_coefficients (vcl_vector< T > const &coeffs) |
| void | print (vcl_ostream &os) const |
| Print this polynomial to stream. | |
Protected Attributes | |
| vcl_vector< T > | coeffs_ |
| The coefficients of the polynomial. | |
Detailed Description
template<class T>
class vnl_polynomial< T >
Evaluation of polynomials.
vnl_polynomial<T> represents a univariate polynomial with coefficients of datatype T, stored as a vector of values. This allows evaluation of the polynomial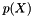 
at given values of 
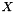, and of its derivative 
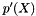or primitive function 
.
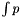The class also provides the common polynomial arithmetic, i.e., + - *, and even long division (through operators / and %).
The coefficients (coeffs_) are stored as a vector, starting with the constant term. Hence coeffs_[n] is the coefficient of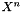 
,
Definition at line 52 of file vnl_polynomial.h.
Constructor & Destructor Documentation
| vnl_polynomial< T >::vnl_polynomial | ( | vcl_vector< T > const & | a | ) | [inline] |
Initialize the polynomial from its coefficients, lowest order first.
The polynomial is ![$ a[d] X^d + a[d-1] X^{d-1} + \cdots + a[0] = 0 $](form_44.png)
. Note that this constructor expects the constant term coefficient first, as opposed to the C array constructor! An assertion makes sure that the input vector is in normalised form, i.e., that it is either empty or that the highest order coefficient is nonzero.
Definition at line 61 of file vnl_polynomial.h.
| vnl_polynomial< T >::vnl_polynomial | ( | T const * | a, |
| unsigned | len | ||
| ) | [inline] |
Initialize polynomial from C array, highest order first.
The parameter len is the number of coefficients passed in, which equals the degree plus one. Note that this constructor expects the highest order coefficients first, as opposed to the std::vector constructor!
Definition at line 68 of file vnl_polynomial.h.
| vnl_polynomial< T >::vnl_polynomial | ( | T const & | a | ) | [inline] |
Initialize polynomial from single value, thus creating a monomial.
This is effectively an implicit cast from type T to class vnl_polynomial, useful when adding or multiplying a polynomial with a number.
Definition at line 73 of file vnl_polynomial.h.
| vnl_polynomial< T >::vnl_polynomial | ( | int | d = -1 | ) | [inline] |
Initialize polynomial of a given degree.
The default constructor initializes to the zero polynomial (which has degree -1). but even with an explicit argument, the polynomial is the zero polynomial (with non-compact storage) so it should always be used in conjunction with operator[] for setting individual coefficients, at least coefficient [d].
Definition at line 80 of file vnl_polynomial.h.
Member Function Documentation
| const vcl_vector<T>& vnl_polynomial< T >::coefficients | ( | ) | const [inline] |
Return the vector of coefficients.
Definition at line 150 of file vnl_polynomial.h.
| vcl_vector<T>& vnl_polynomial< T >::coefficients | ( | ) | [inline] |
Return the vector of coefficients.
Definition at line 152 of file vnl_polynomial.h.
| int vnl_polynomial< T >::degree | ( | ) | const [inline] |
Return the degree (highest power of X) of the polynomial.
If the polynomial is zero, the degree is effectively -1. Note that this method assumes a compactified representation, i.e., one where the highest order coefficient is non-zero. Otherwise, the value returned by degree() will be larger than the degree.
Definition at line 142 of file vnl_polynomial.h.
| vnl_polynomial< T > vnl_polynomial< T >::derivative | ( | ) | const |
Return derivative of this polynomial.
Definition at line 106 of file vnl_polynomial.txx.
| T vnl_polynomial< T >::devaluate | ( | T const & | x | ) | const [inline] |
Evaluate derivative at value x.
Definition at line 120 of file vnl_polynomial.h.
| T vnl_polynomial< T >::evaluate | ( | T const & | x | ) | const |
Evaluate polynomial at value x.
Evaluate polynomial at value x.
Definition at line 19 of file vnl_polynomial.txx.
| T vnl_polynomial< T >::evaluate_integral | ( | T const & | x | ) | const [inline] |
Evaluate integral at x (assuming constant of integration is zero).
Beware that this operation might not make sense for integral types T!
Definition at line 129 of file vnl_polynomial.h.
| T vnl_polynomial< T >::evaluate_integral | ( | T const & | x1, |
| T const & | x2 | ||
| ) | const [inline] |
Evaluate integral between x1 and x2.
Beware that this operation might not make sense for integral types T!
Definition at line 133 of file vnl_polynomial.h.
| vnl_polynomial< T > vnl_polynomial< T >::operator% | ( | vnl_polynomial< T > const & | f | ) | const |
Returns polynomial which is the remainder after a long division by polynomial f.
Returns polynomial which is the remainder after long division by f.
Beware that this operation might not make sense for integral types T if the highest order coefficient of f is not 1 or -1!
Definition at line 91 of file vnl_polynomial.txx.
| vnl_polynomial<T>& vnl_polynomial< T >::operator%= | ( | vnl_polynomial< T > const & | f | ) | [inline] |
Definition at line 111 of file vnl_polynomial.h.
| vnl_polynomial< T > vnl_polynomial< T >::operator* | ( | vnl_polynomial< T > const & | f | ) | const |
Returns polynomial which is product of this with polynomial f.
Definition at line 58 of file vnl_polynomial.txx.
| vnl_polynomial<T>& vnl_polynomial< T >::operator*= | ( | vnl_polynomial< T > const & | f | ) | [inline] |
Definition at line 109 of file vnl_polynomial.h.
| vnl_polynomial< T > vnl_polynomial< T >::operator+ | ( | vnl_polynomial< T > const & | f | ) | const |
Returns polynomial which is sum of this with polynomial f.
Definition at line 44 of file vnl_polynomial.txx.
| vnl_polynomial<T>& vnl_polynomial< T >::operator+= | ( | vnl_polynomial< T > const & | f | ) | [inline] |
Definition at line 107 of file vnl_polynomial.h.
| vnl_polynomial< T > vnl_polynomial< T >::operator- | ( | ) | const |
Returns negative of this polynomial.
Definition at line 34 of file vnl_polynomial.txx.
| vnl_polynomial<T> vnl_polynomial< T >::operator- | ( | vnl_polynomial< T > const & | f | ) | const [inline] |
Returns polynomial which is difference of this with polynomial f.
Definition at line 92 of file vnl_polynomial.h.
| vnl_polynomial<T>& vnl_polynomial< T >::operator-= | ( | vnl_polynomial< T > const & | f | ) | [inline] |
Definition at line 108 of file vnl_polynomial.h.
| vnl_polynomial< T > vnl_polynomial< T >::operator/ | ( | vnl_polynomial< T > const & | f | ) | const |
Returns polynomial which is the result of the long division by polynomial f.
Returns polynomial which is the result of a long division by f.
Beware that this operation might not make sense for integral types T if the highest order coefficient of f is not 1 or -1!
Definition at line 73 of file vnl_polynomial.txx.
| vnl_polynomial<T>& vnl_polynomial< T >::operator/= | ( | vnl_polynomial< T > const & | f | ) | [inline] |
Definition at line 110 of file vnl_polynomial.h.
| bool vnl_polynomial< T >::operator== | ( | vnl_polynomial< T > const & | p | ) | const [inline] |
comparison operator.
Definition at line 83 of file vnl_polynomial.h.
| T& vnl_polynomial< T >::operator[] | ( | unsigned int | i | ) | [inline] |
Access to the polynomial coefficient of $X^i$.
Definition at line 145 of file vnl_polynomial.h.
| T vnl_polynomial< T >::operator[] | ( | unsigned int | i | ) | const [inline] |
Access to the polynomial coefficient of $X^i$.
Definition at line 147 of file vnl_polynomial.h.
| vnl_polynomial< T > vnl_polynomial< T >::primitive | ( | ) | const |
Return primitive function (inverse derivative) of this polynomial.
Since a primitive function is not unique, the one with constant term 0 is returned. Beware that this operation might not make sense for integral types T!
Since a primitive function is not unique, the one with constant = 0 is returned Beware that this operation might not make sense for integral types T!
Definition at line 120 of file vnl_polynomial.txx.
| void vnl_polynomial< T >::print | ( | vcl_ostream & | os | ) | const |
Print this polynomial to stream.
Definition at line 132 of file vnl_polynomial.txx.
| void vnl_polynomial< T >::set_coefficients | ( | vcl_vector< T > const & | coeffs | ) | [inline] |
Definition at line 154 of file vnl_polynomial.h.
Member Data Documentation
vcl_vector<T> vnl_polynomial< T >::coeffs_ [protected] |
The coefficients of the polynomial.
coeffs_.front() is the const term. coeffs_[n] is the coefficient of the 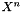term
Definition at line 163 of file vnl_polynomial.h.
The documentation for this class was generated from the following files:
- core/vnl/vnl_polynomial.h
- core/vnl/vnl_polynomial.txx
