Fits a conic to a set of points using linear regression. More...
#include <vcl_vector.h>#include <vcl_iostream.h>#include <vnl/vnl_matrix_fixed.h>#include <vgl/vgl_point_2d.h>#include <vgl/vgl_homg_point_2d.h>#include <vgl/vgl_conic.h>#include <vgl/algo/vgl_norm_trans_2d.h>Go to the source code of this file.
Classes | |
| class | vgl_conic_2d_regression< T > |
Defines | |
| #define | VGL_CONIC_2D_REGRESSION_INSTANTIATE(T) extern "please include vgl/algo/vgl_conic_2d_regression.txx first" |
Detailed Description
Fits a conic to a set of points using linear regression.
- Date:
- June 17, 2005
Since conic fitting is rather ill-conditioned it is necessary to normalize the point coordinates so that they have equal standard deviations with respect to the center (mean) of the pointset. The points are transformed to have zero mean. The resulting conic is transformed back to the original frame for computing the Sampson approximation to fitting error.
The regression uses the Bookstein algorithm which constrains the conic norm, 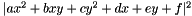 , so that
, so that 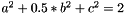 With this normalization, the resulting fit is invariant up to a similarity transform of the pointset. The solution is formulated as an eigenvalue problem as follows:
With this normalization, the resulting fit is invariant up to a similarity transform of the pointset. The solution is formulated as an eigenvalue problem as follows:
The scatter matrix S is decomposed as
$ S = {array}{cc} S_{11} & S_{12} \ S_{21} & S_{22} {array}$ note 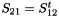
The conic coefficients are 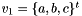 and
and 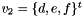 The Bookstein constraint is expressed by the diagonal matrix D = Diag{1, 0.5, 1, 0, 0, 0} The Lagrangian to be minimized is $ L = v_1^t S_{11} v_1 + 2 v_2^t S_{21} v_1 + v_2^t S_{22} v_2
The Bookstein constraint is expressed by the diagonal matrix D = Diag{1, 0.5, 1, 0, 0, 0} The Lagrangian to be minimized is $ L = v_1^t S_{11} v_1 + 2 v_2^t S_{21} v_1 + v_2^t S_{22} v_2
- (v_1^t D v_1 -2) $.
Minimizing with respect to v2 gives 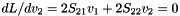
So, 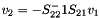 .
.
Substituting for v2 in L,
$ L = v_1^t ( S_{11} - S_{12} * S_{22}^-1 * S_{21}) v_1 - (v_1^t D v_1 -2) = v_1^t ( (S_{11} - S_{12} * S_{22}^-1 * S_{21}) - D ) v_1 - 2 $,
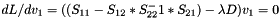 .
.
So, 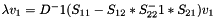 .
.
This eigenvalue problem is solved using singular value decomposition.
Modifications
none
Definition in file vgl_conic_2d_regression.h.
Define Documentation
| #define VGL_CONIC_2D_REGRESSION_INSTANTIATE | ( | T | ) | extern "please include vgl/algo/vgl_conic_2d_regression.txx first" |
Definition at line 149 of file vgl_conic_2d_regression.h.
 1.7.5.1
1.7.5.1