Generates random samples from an Epanechnikov kernel estimate. More...
#include <pdf1d_epanech_kernel_pdf_sampler.h>
Public Member Functions | |
| pdf1d_epanech_kernel_pdf_sampler () | |
| Dflt ctor. | |
| virtual | ~pdf1d_epanech_kernel_pdf_sampler () |
| Destructor. | |
| const pdf1d_epanech_kernel_pdf & | epanech_kernel_pdf () const |
| virtual double | sample () |
| Draw random sample from distribution. | |
| virtual void | regular_samples (vnl_vector< double > &x) |
| Fill x with samples possibly chosen so as to represent the distribution. | |
| virtual void | reseed (unsigned long) |
| Reseeds the static random number generator (one per derived class). | |
| short | version_no () const |
| Version number for I/O. | |
| virtual vcl_string | is_a () const |
| Name of the class. | |
| virtual bool | is_class (vcl_string const &s) const |
| Does the name of the class match the argument?. | |
| virtual pdf1d_sampler * | clone () const |
| Create a copy on the heap and return base class pointer. | |
| const pdf1d_pdf & | model () const |
| PDF of which this is an instance. | |
| virtual void | set_model (const pdf1d_pdf &) |
| Set model for which this is an instance. | |
| virtual void | get_samples (vnl_vector< double > &x) |
| Fill x with samples drawn from distribution. | |
| virtual void | regular_samples_and_prob (vnl_vector< double > &x, vnl_vector< double > &p) |
| Fill x with samples possibly chosen so as to represent the distribution. | |
| virtual void | print_summary (vcl_ostream &os) const |
| Print class to os. | |
Static Public Member Functions | |
| static double | epan_transform (double x) |
| Transform a unit uniform distribution x into an Epanech distribution y. | |
Protected Attributes | |
| vnl_random | rng_ |
| The random number generator. | |
| const pdf1d_pdf * | pdf_model_ |
Detailed Description
Generates random samples from an Epanechnikov kernel estimate.
Definition at line 15 of file pdf1d_epanech_kernel_pdf_sampler.h.
Constructor & Destructor Documentation
| pdf1d_epanech_kernel_pdf_sampler::pdf1d_epanech_kernel_pdf_sampler | ( | ) |
Dflt ctor.
Definition at line 17 of file pdf1d_epanech_kernel_pdf_sampler.cxx.
| pdf1d_epanech_kernel_pdf_sampler::~pdf1d_epanech_kernel_pdf_sampler | ( | ) | [virtual] |
Destructor.
Definition at line 22 of file pdf1d_epanech_kernel_pdf_sampler.cxx.
Member Function Documentation
| pdf1d_sampler * pdf1d_epanech_kernel_pdf_sampler::clone | ( | ) | const [virtual] |
Create a copy on the heap and return base class pointer.
Implements pdf1d_sampler.
Definition at line 148 of file pdf1d_epanech_kernel_pdf_sampler.cxx.
| double pdf1d_epanech_kernel_pdf_sampler::epan_transform | ( | double | x | ) | [static] |
Transform a unit uniform distribution x into an Epanech distribution y.
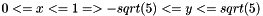 Matlab found 6 solutions to
Matlab found 6 solutions to 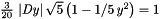 The 6th, which has the correct properties is $-1/2\, [3]{-10\, {5}x+5\, {-5+20\,{x}^{2}}}-5/2\, { {1}{ [3]{-10\, {5}x+5\, {-5+20\,{x}^{2}}}}}-1/2\, {-1} {3} ( [3]{-10\, {5}x+5\, {-5+20\, {x}^{2}}}-5\,{ {1}{ [3]{-10\, {5}x+5\, {-5+20\, {x}^{2}}}}} )$
The 6th, which has the correct properties is $-1/2\, [3]{-10\, {5}x+5\, {-5+20\,{x}^{2}}}-5/2\, { {1}{ [3]{-10\, {5}x+5\, {-5+20\,{x}^{2}}}}}-1/2\, {-1} {3} ( [3]{-10\, {5}x+5\, {-5+20\, {x}^{2}}}-5\,{ {1}{ [3]{-10\, {5}x+5\, {-5+20\, {x}^{2}}}}} )$
Definition at line 48 of file pdf1d_epanech_kernel_pdf_sampler.cxx.
| const pdf1d_epanech_kernel_pdf & pdf1d_epanech_kernel_pdf_sampler::epanech_kernel_pdf | ( | ) | const |
Definition at line 28 of file pdf1d_epanech_kernel_pdf_sampler.cxx.
| void pdf1d_sampler::get_samples | ( | vnl_vector< double > & | x | ) | [virtual, inherited] |
Fill x with samples drawn from distribution.
Definition at line 45 of file pdf1d_sampler.cxx.
| vcl_string pdf1d_epanech_kernel_pdf_sampler::is_a | ( | ) | const [virtual] |
Name of the class.
Reimplemented from pdf1d_sampler.
Definition at line 127 of file pdf1d_epanech_kernel_pdf_sampler.cxx.
| bool pdf1d_epanech_kernel_pdf_sampler::is_class | ( | vcl_string const & | s | ) | const [virtual] |
Does the name of the class match the argument?.
Reimplemented from pdf1d_sampler.
Definition at line 134 of file pdf1d_epanech_kernel_pdf_sampler.cxx.
| const pdf1d_pdf & pdf1d_sampler::model | ( | ) | const [inherited] |
PDF of which this is an instance.
Definition at line 38 of file pdf1d_sampler.cxx.
| void pdf1d_sampler::print_summary | ( | vcl_ostream & | os | ) | const [virtual, inherited] |
Print class to os.
Definition at line 101 of file pdf1d_sampler.cxx.
| void pdf1d_epanech_kernel_pdf_sampler::regular_samples | ( | vnl_vector< double > & | x | ) | [virtual] |
Fill x with samples possibly chosen so as to represent the distribution.
Samples equal numbers from each kernel.
Reimplemented from pdf1d_sampler.
Definition at line 85 of file pdf1d_epanech_kernel_pdf_sampler.cxx.
| void pdf1d_sampler::regular_samples_and_prob | ( | vnl_vector< double > & | x, |
| vnl_vector< double > & | p | ||
| ) | [virtual, inherited] |
Fill x with samples possibly chosen so as to represent the distribution.
As regular_samples(x), but p[i] is set to p(x[i])
By default simply randomly sample from distribution
Definition at line 65 of file pdf1d_sampler.cxx.
| void pdf1d_epanech_kernel_pdf_sampler::reseed | ( | unsigned long | seed | ) | [virtual] |
Reseeds the static random number generator (one per derived class).
Implements pdf1d_sampler.
Definition at line 120 of file pdf1d_epanech_kernel_pdf_sampler.cxx.
| double pdf1d_epanech_kernel_pdf_sampler::sample | ( | ) | [virtual] |
Draw random sample from distribution.
Implements pdf1d_sampler.
Definition at line 65 of file pdf1d_epanech_kernel_pdf_sampler.cxx.
| void pdf1d_sampler::set_model | ( | const pdf1d_pdf & | model | ) | [virtual, inherited] |
Set model for which this is an instance.
Reimplemented in pdf1d_mixture_sampler, pdf1d_exponential_sampler, pdf1d_flat_sampler, and pdf1d_gaussian_sampler.
Definition at line 32 of file pdf1d_sampler.cxx.
| short pdf1d_epanech_kernel_pdf_sampler::version_no | ( | ) | const |
Version number for I/O.
Definition at line 141 of file pdf1d_epanech_kernel_pdf_sampler.cxx.
Member Data Documentation
const pdf1d_pdf* pdf1d_sampler::pdf_model_ [protected, inherited] |
Definition at line 26 of file pdf1d_sampler.h.
vnl_random pdf1d_epanech_kernel_pdf_sampler::rng_ [protected] |
The random number generator.
Definition at line 19 of file pdf1d_epanech_kernel_pdf_sampler.h.
The documentation for this class was generated from the following files:
- contrib/mul/pdf1d/pdf1d_epanech_kernel_pdf_sampler.h
- contrib/mul/pdf1d/pdf1d_epanech_kernel_pdf_sampler.cxx
 1.7.5.1
1.7.5.1