#include "vgui_draw_line.h"#include <vgui/vgui_gl.h>#include <vgui/internals/vgui_multiply_4x4.h>#include <vgui/internals/vgui_transpose_4x4.h>Go to the source code of this file.
Defines | |
| #define | dot4(a, b) ((a)[0]*(b)[0] + (a)[1]*(b)[1] + (a)[2]*(b)[2] + (a)[3]*(b)[3]) |
| #define | l_c4(a, x, b, y, ax_plus_by) { for (int i=0; i<4; ++i) (ax_plus_by)[i] = (a)*(x)[i] + (b)*(y)[i]; } |
| #define | dot3(a, b) ((a)[0]*(b)[0] + (a)[1]*(b)[1] + (a)[2]*(b)[2]) |
| #define | cross3(a, b, c) |
| #define | add3(a, b, c) { for (int i=0; i<3; ++i) (c)[i] = (a)[i] + (b)[i]; } |
| #define | sub3(a, b, c) { for (int i=0; i<3; ++i) (c)[i] = (a)[i] - (b)[i]; } |
| #define | trace(str) |
Functions | |
| bool | vgui_draw_line (double const T[4][4], double const X[4], double const Y[4]) |
| draw infinite line spanned in space by two points. | |
| bool | vgui_draw_line (double const P[4][4], double const M[4][4], double const X[4], double const Y[4]) |
| draw infinite line spanned in space by two points. | |
| bool | vgui_draw_line (double const X[4], double const Y[4]) |
| draw infinite line spanned in space by two points (easy). | |
| bool | vgui_draw_line (double const T[4][4], double a, double b, double c) |
| draw infinite line $ax+by+cw=0, z=0$ from total projection matrix $T=P M$. | |
| bool | vgui_draw_line (double const P[4][4], double const M[4][4], double a, double b, double c) |
| draw infinite line $ax+by+cw=0, z=0$ from projection and modelview matrices, P and M. | |
| bool | vgui_draw_line (double a, double b, double c) |
| draw infinite line $ax+by+cw=0, z=0$ (easy). | |
Detailed Description
Definition in file vgui_draw_line.cxx.
Define Documentation
| #define add3 | ( | a, | |
| b, | |||
| c | |||
| ) | { for (int i=0; i<3; ++i) (c)[i] = (a)[i] + (b)[i]; } |
Definition at line 113 of file vgui_draw_line.cxx.
| #define cross3 | ( | a, | |
| b, | |||
| c | |||
| ) |
{ \
(c)[0] = (a)[1]*(b)[2] - (a)[2]*(b)[1]; \
(c)[1] = (a)[2]*(b)[0] - (a)[0]*(b)[2]; \
(c)[2] = (a)[0]*(b)[1] - (a)[1]*(b)[0]; \
}
Definition at line 108 of file vgui_draw_line.cxx.
| #define dot3 | ( | a, | |
| b | |||
| ) | ((a)[0]*(b)[0] + (a)[1]*(b)[1] + (a)[2]*(b)[2]) |
Definition at line 107 of file vgui_draw_line.cxx.
| #define dot4 | ( | a, | |
| b | |||
| ) | ((a)[0]*(b)[0] + (a)[1]*(b)[1] + (a)[2]*(b)[2] + (a)[3]*(b)[3]) |
Definition at line 16 of file vgui_draw_line.cxx.
| #define l_c4 | ( | a, | |
| x, | |||
| b, | |||
| y, | |||
| ax_plus_by | |||
| ) | { for (int i=0; i<4; ++i) (ax_plus_by)[i] = (a)*(x)[i] + (b)*(y)[i]; } |
Definition at line 17 of file vgui_draw_line.cxx.
| #define sub3 | ( | a, | |
| b, | |||
| c | |||
| ) | { for (int i=0; i<3; ++i) (c)[i] = (a)[i] - (b)[i]; } |
Definition at line 114 of file vgui_draw_line.cxx.
| #define trace | ( | str | ) |
Definition at line 115 of file vgui_draw_line.cxx.
Function Documentation
| bool vgui_draw_line | ( | double const | T[4][4], |
| double const | X[4], | ||
| double const | Y[4] | ||
| ) |
draw infinite line spanned in space by two points.
From total projection matrix 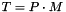 .
.
Definition at line 19 of file vgui_draw_line.cxx.
| bool vgui_draw_line | ( | double const | P[4][4], |
| double const | M[4][4], | ||
| double const | X[4], | ||
| double const | Y[4] | ||
| ) |
draw infinite line spanned in space by two points.
From projection and modelview matrices, P and M.
Definition at line 88 of file vgui_draw_line.cxx.
| bool vgui_draw_line | ( | double const | X[4], |
| double const | Y[4] | ||
| ) |
draw infinite line spanned in space by two points (easy).
Definition at line 95 of file vgui_draw_line.cxx.
| bool vgui_draw_line | ( | double const | T[4][4], |
| double | a, | ||
| double | b, | ||
| double | c | ||
| ) |
draw infinite line $ax+by+cw=0, z=0$ from total projection matrix $T=P M$.
Definition at line 117 of file vgui_draw_line.cxx.
| bool vgui_draw_line | ( | double const | P[4][4], |
| double const | M[4][4], | ||
| double | a, | ||
| double | b, | ||
| double | c | ||
| ) |
draw infinite line $ax+by+cw=0, z=0$ from projection and modelview matrices, P and M.
Definition at line 200 of file vgui_draw_line.cxx.
| bool vgui_draw_line | ( | double | a, |
| double | b, | ||
| double | c | ||
| ) |
draw infinite line $ax+by+cw=0, z=0$ (easy).
Definition at line 207 of file vgui_draw_line.cxx.
 1.7.5.1
1.7.5.1